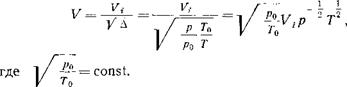СЛУЧАЙНЫЕ ПОГРЕШНОСТИ

Перейдем теперь к рассмотрению случайных погрешностей. Напомним вкратце основные положения теории случайных по­грешностей, разработанной применительно к совокупности по­грешностей, возникающих при повторном многократном измере­нии одной и той же величины.

Случайным погрешностям приписывают следующие два свойства:

1. При большом числе измерений одинаково часто встреча­ются погрешности равные по величине, но противоположные по знаку, т. е. число положительных и отрицательных погрешностей одинаково.

2. Малые погрешности встречаются чаще, чем большие.

При большом числе измерений применим так называемый з а-

кон нормального распределения случайных по­грешностей, заключающийся в следующем. Обозначим через dP вероятность появления погрешности, значение которой заклю­чается в интервале 8 и 8+d8. Тогда по закону нормального рас­пределения

dP=y d8,

где

82

Величина у называется частотой появления случай­ных погрешностей, а с — средней квадратичной по­грешностью ряда измерений. На фиг. 3. 1 приведена так на­зываемая кривая вероятности у=/(8), соответствующая уравнению (3. 1) для трех значений о.

Для того чтобы определить величину о для рассматривае­мой серии измерений, поступают следующим образом. Пусть при измерении, произведенном п раз в одинаковых условиях одним и тем же прибором, были получены следующие результаты:

Вероятнейшее значение L измеряемой величины равно средне­му арифметическому из полученных значений, т. е.

^ . .4-/я

П

Если истинное значение измеряемой величины равно X, a U — каждое из п значений, полученных при измерении, то величина

Si = U—X

является случайной погрешностью измерения, а ве­личина

Vi —U—L

называется остаточной погрешностью.

Средняя квадратичная погрешность п измерений определяет­ся формулой

j

■у

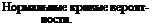
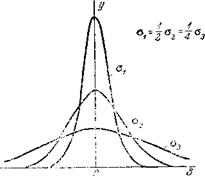В курсах теории вероятности доказывается, что при неогра­ниченном увеличении числа измерений п величина о, опреде­ляемая по формуле (3. 3), стре­мится к значению средней квадратичной ошибки с, фигу­рирующей в законе нормаль­ного распределения [формула (3.1)].

Средняя квадратичная по­грешность ряда измерений х а — рактеризует точность измерений. Из фиг. 3. 1 видно, что меньшему значению с со­ответствует преобладание ма­лых случайных погрешностей и, следовательно, большая точ­ность измерения данной вели­чины; наоборот, при большом значении о большие случай­ные погрешности встречаются чаще, а значит точность измере­ния ниже.

Для определения средней квадратичной погрешности с по формуле (3. 3) нужно знать истинное значение измеряемой ве­личины X. Так как обычно оно неизвестно, а на основе измерений определяется среднее арифметическое L и могут быть опреде­лены только остаточные погрешности каждого измерения vif то для определения а пользуются формулами, в которых подсчет С ведется через Vi — В случае ограниченного числа измерений [4]
приближенное значение средней квадратичной погрешности о может быть найдено по формуле Бесселя через остаточные по­грешности Vi, значения которых просто определяются по экспе­риментальным данным измерений

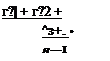
(3.4)

Кроме величины о, точность многократного эксперимен­та характеризуется так называемой вероятной погреш­ностью ряда измерений р, имеющей такую величину, что по­ловина всех случайных погрешностей при повторных измерениях меньше р, а половина больше.

Из теории вероятностей известно, что вероятная и средняя квадратичная погрешности связаны простой зависимостью

р * 4-с — (3-5)

о

Наконец, точность измерений характеризуют еще предель­ной погрешностью ряда измерений $Um, причем

511т = 3з»4,5р. (3.6)

Теоретически доказывается, что при 370 повторных измерениях

вероятно, что только одна погрешность по абсолютной величине больше Bllm.

Как средняя квадратичная, так и вероятная и предельная по­грешности могут служить для характеристики точности изме­рений.

Мы до сих пор рассматривали параметры с, о и 3Ига, ха­рактеризующие точность процесса измерений. В теории случайных ошибок показывается, что точность результа-

т а измерений (т. е. арифметического среднего) может быть оце­нена одним из следующих параметров:

1) средней квадратичной погрешностью ре­зультата среднего арифметического S, равной

(3.7)

где п — число измерении;

2) вероятной погрешностью результата/?

0,6745сг г

у п у п’

3) предельной погрешностью результата ilim:

(3.9)

Для вычисления погрешностей результата S и R по величине остаточных погрешностей применяются следующие формулы:

Необходимо точно уяснить себе разницу между точностью процесса измерений и точностью результата измерений. Точность процесса измерений характеризует степень достовер­ности результата отдельного (единичного) измерения, в то вре­мя как точность результата измерений характеризует точность, с которой определена измеряемая величина, полученная как среднее арифметическое из нескольких измерений. Предположим, например, что нам нужно определить максимальную скорость полета на какой-либо заданной высоте, причем вероятная по­грешность процесса измерений равна р = 1%>. Последнее озна­чает, что если в качестве величины максимальной скорости мы примем величину, определенную из отдельного (единичного’) экс­перимента, то равновероятно, что погрешность будет как мень­ше, так и больше 1%. Если же для определения величины макси­мальной скорости мы произведем четыре замера и примем в качестве величины скорости среднее арифметическое из этих че­тырех замеров, то вероятная погрешность полученного резуль­тата равна по формуле (3. 8)

0,5%.

Следовательно, в этом случае равновероятно, ‘что погрешность найденной величины Етах будет как больше, так и меньше 0,5% (а не 1°/о, как это мы имели бы для единичного измерения).

Из формул для S и R видно-, что, увеличивая число измере­ний, мы повышаем точность результата. Однако для существен­ного повышения точности результата число измерений должно быть увеличено во много раз. Таким образом повышение точ­ности результата путем увеличения числа измерений сопряжено* с большой дополнительной затратой труда и времени.

В технической практике для оценки точности результата из­мерений, а также процесса измерений обычно применяют пре­дельную погрешность. Однако в ряде случаев применяются как средняя квадратичная погрешность (особенно для оценки точ­ности процесса измерений), так и вероятная погрешность (осо­бенно для оценки точности результата измерений). Вследствие этого во — избежание недоразумений нужно всегда, говоря о точ­ности эксперимента или прибора, указывать, какой параметр принят для ее оценки.

4І:

Результат измерения обычна принято представлять в виде записи следующего вида:

X — CL~~b,

где а — результат измерения, а b — погрешность результата (ве­роятная или предельная). Если написано

V=752+9 км/час,

где 9 км/час=ит— предельная погрешность, то эту запись мы должны понимать так: приняв в качестве значения скорости са­молета 752 км/час, мы допускаем при этом погрешность, едва ли превышающую 9 км/час. Если

V=752+2 км/час,

где 2 км/час^Я — вероятная погрешность, то такую запись нуж­но понимать следующим образом: приняв в качестве значения скорости самолета 752 км/час, мы допускаем погрешность, кото­рая в равной степени может быть по абсолютной величине как больше», так и меньше 2 км/час, но едва ли превысит Х1ітя^4,5R = = 4,5 -2 = 9 км/час в соответствии с формулой (3.9).

При округлении результатов измерений следует руковод­ствоваться их погрешностями. Обычно округление производится таким образом, чтобы только последняя значащая цифра была сомнительна. Так, в приведенном выше примере, получив при обработке 752,4 км/час, мы округляем до ближайшего целого числа и пишем 752 км/час. Если принять при определении цент­ровки самолета предельную погрешность в 0,8% средней аэро­динамической хорды, то результат центровки имеет смысл запи­сывать лишь с одним десятичным знаком, например, 23,6% САХ вместо 23,57% САХ.

Приведенные вами выше формулы относятся к случаю непо­средственного (прямого) измерения величины. Рассмотрим те­перь случай косвенного измерения величин, с которым обычно приходится иметь дело в практике испытаний. Пусть нам необходимо определить величину

и = и(х, у, г),

где х, у, z — величины, измеряемые непосредственно. В теории случайных погрешностей доказывается, что средняя квад­ратичная погрешность ряда косвенных изме­рений равна

где сх, су, оz — соответствующие средние квадратичные погреш­ности ряда прямых измерений величин х, у и z. Аналогичные формулы могут быть написаны и для вероятной или предельной погрешности ряда косвенных измерений. Эти формулы называют законом сложения средних погрешностей.

Часто вместо абсолютной погрешности, выраженной в еди­ницах измеряемой величины, пользуются относительной погрешностью, выраженной в долях значения измеряемой величины. Относительные погрешности, являющиеся отвлечен­ными числами, мы будем обозначать теми же буквами, что и абсолютные, но с индексом 0 внизу:

Guo=-f> = и т. д.

Закон сложения средних погрешностей в случае применения относительных погрешностей можно написать в следующем виде:

Gu0—^ u‘iGlo+uy°lo + ul~lo’ (3.13)

где

_ х ди _ у ди z dz

х и дх ’ у и ду “ и ди

(в дальнейшем величины этого вида будем называть показа­телями). Выражения вида ихсх о называются частными погрешностями косвенного измерения.

Для часто встречающейся на практике степенной зависи­мости измеряемой величины от нескольких аргументов вида

и — kxaybz°, (3.14)

получаем

°а0 = + ^2ау0 + c2°z0 * (3. 15)

Применим формулу (3. 15) для определения средней квадра­тичной погрешности измерения истинной скорости, определяемой при летных испытаниях по формуле вида (3. 14)

Пусть средние квадратичные относительные погрешности из­мерений Vi, р и Т равны соответственно 0,5%; 0,1%; 0,3%. По формуле (3.15) получим

аКо=| f 0,52+-Г-0ЛЧ -Г-0,32 ж 0,524%.

Этот пример показывает, что если одна из частных погрешно­стей косвенного измерения значительно превышает остальные, то результирующая точность близка к этой частной погрешности. Поэтому для повышения точности особое внимание сле­дует уделять уменьшению погрешности того измерения, котор О’е обладает наибольшей ча­стной погрешностью. Так, в приведенном примере для повышения точности измерения истинной скорости следует су­щественно повысить точность измерения индикаторной скорости, повышение же точности измерения давления или температуры мало скажется на точности результата.

Если точность определения величины и обусловлена несколь­кими не зависимыми друг от друга источниками случайных по­грешностей, причем известны соответствующие этим источникам средние погрешности о і, о 2, с3, то средняя погрешность вели­чины и определяется по квадратичному закону

(3.16)

Так, например, точность измерения давления воздуха в полете обусловлена точностью барографа (сі), точностью поправки на искажение статического давления в месте установки приемника давления на самолете ( а2), точностью поправки на запаздывание показаний самописца (а3) и т. п. Учитывая, что перечисленные источники погрешностей не зависят друг от друга, точность из­мерения давления воздуха можно оценить по формуле (3. 16).